

We propose a novel Augmented Mass-Spring (AMS) model for real-time simulation of dense hair at strand level. Our approach considers the traditional edge, bending, and torsional degrees of freedom in mass-spring systems, but incorporates an additional one-way biphasic coupling with a ghost rest-shape configuration. Trough multiple evaluation experiments with varied dynamical settings, we show that AMS improves the stability of the simulation in comparison to mass-spring discretizations, preserves global features, and enables the simulation of non-Hookean effects. Using an heptadiagonal decomposition of the resulting matrix, our approach provides the efficiency advantages of mass-spring systems over more complex constitutive hair models, while enabling a more robust simulation of multiple strand configurations. Finally, our results demonstrate that our framework enables the generation, complex interactivity, and editing of simulation-ready dense hair assets in real-time.
We consider the basic edge, bending, and torsion springs, for which an uniform spring constant \( \kappa_{L} \) is used, as well as a weakly interaction with a ghost rest-shape via one-way springs that connect each particle with their corresponding ghost in the rest configuration
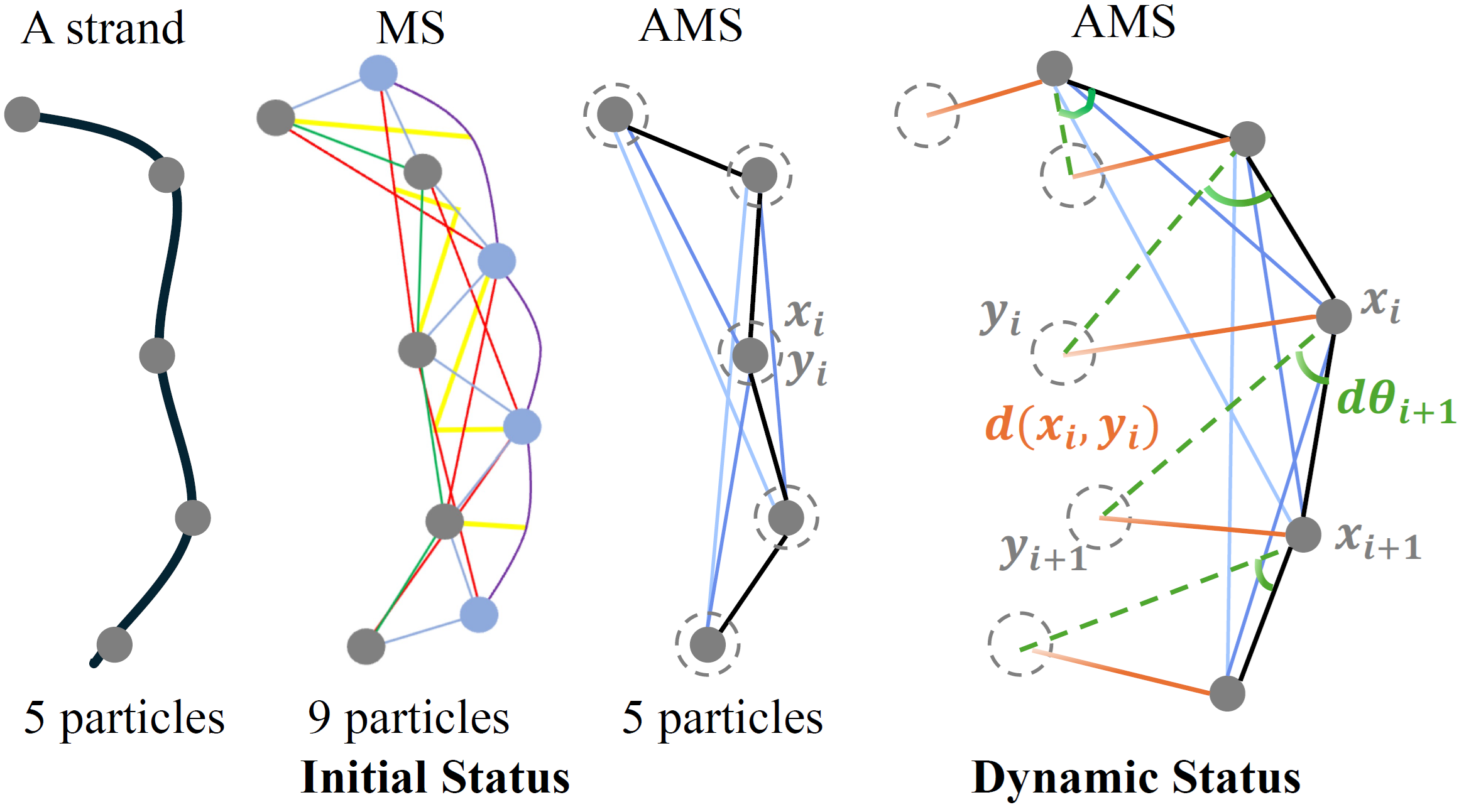
We implement an integrity spring, with stiffness \( \kappa_{I} \), and tension proportional to the deviation distance between a particle and its ghost; we also use an angular spring, with stiffness \(\kappa_{\alpha}\), and tension proportional to the deviation angle \(d\theta\). Together, these springs form the biphasic connection between the ghost rest-shape and the simulated strand.
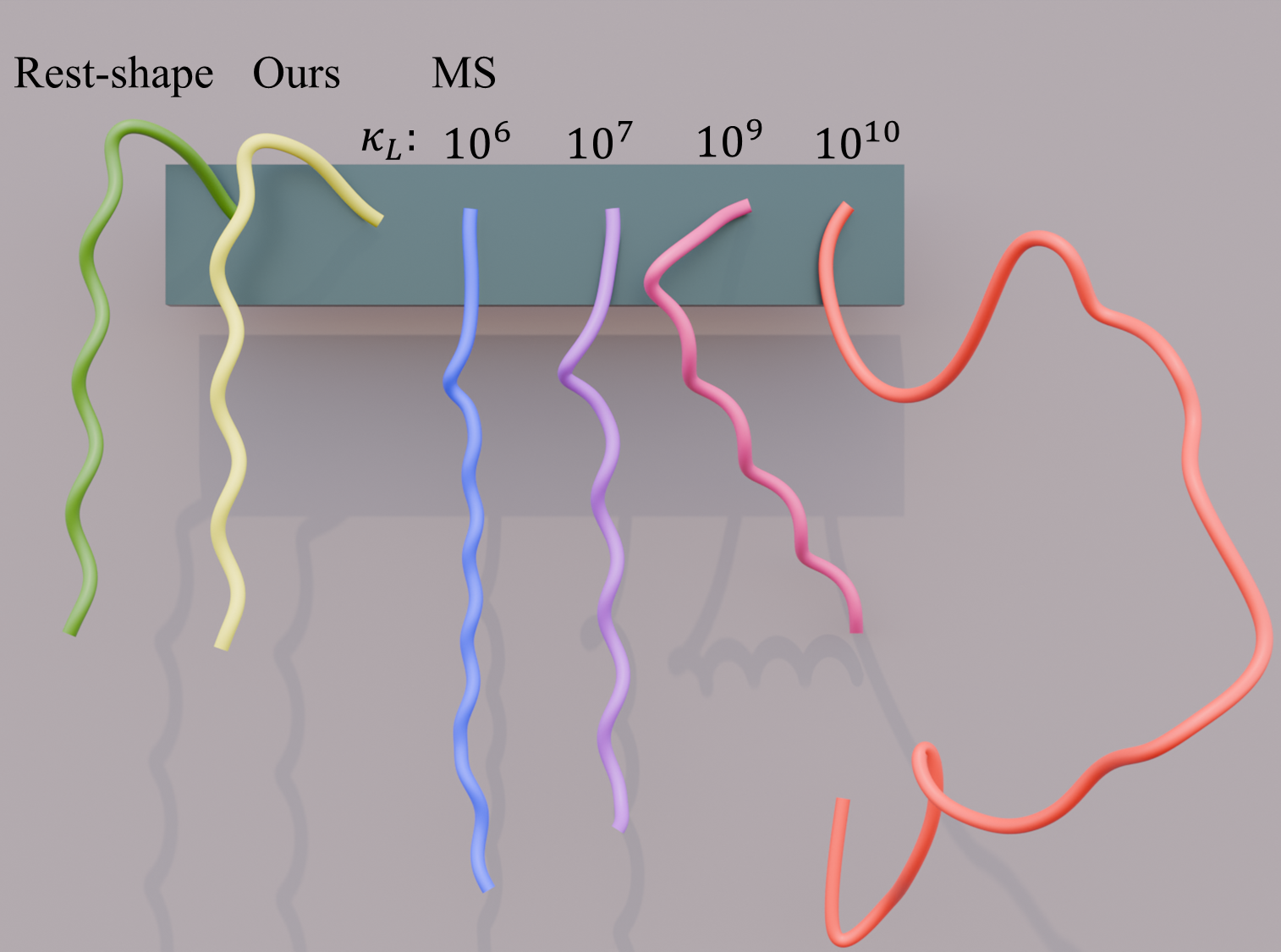
We asses the impact of couplings in our biphasic interaction model. Left: Simulation of a single strand using our method and MS starting from a rest shape. Our model preserves global features, while MS fails to maintain shape, becoming unstable as \(\kappa_{L}\) increases. Right: Wisp simulation under decreasing angular coupling values. Instability grows as \(\kappa_{\alpha}\) decreases, collapsing entirely at \(\kappa_{\alpha} = 0\), where our method converges to MS.

Using the Wig model of Luo et. al. under similar wind conditions, Hsu et. al. achieves 1.2 ms/frame for 1024 strands, while our method runs at 0.04 ms for the same setup. For higher fidelity, we simulate 10,422 strands (full asset) at 1.9 ms/frame. Unlike Hsu et. al., our approach avoids sagging-specific initialization while maintaining stability.
To reduce computational costs, prior works often interpolate from a limited set of guide strands, but this can cause artifacts in complex interactions. Here we show hair-hand interactions with 15k simulated strands and Linear Hair Skinning (LHS) using 2048 guides.

We demonstrate the effectiveness of our framework in simulating facial hair. Traditional MS is not able to capture the behavior of strands of different lengths because global features are not considered, and the general shape of the hair is lost after initialization. As a result, all strands behave similarly regardless of their length, decreasing the simulation fidelity for complex structures such as beards and moustaches. Additionally, more complex models like DER also struggle with facial hair since they require using extremely stiff strands to maintain the desired structure of this type of hair. Our framework is able to overcome these limitations, preserving the structure and character of facial hair with minimal adjustments.
We show the simulation of an asymmetric hairstyle using our scheme. The distinct dynamics of each section are accurately captured, demonstrating the versatility of our approach for non-standard hairstyles.
Here, we demonstrate the progressive hair shape change as strands undergo the intense acceleration of a roller-coaster. Our framework effectively preserves the initial hairstyle and captures the post-ride hair scramble by parametrizing non-Hookean responses in the integrity coupling of the biphasic interaction.
We present live demonstrations of our framework alongside offline renderings derived from similar simulations. First, we show digital grooming.

Finally, we demonstrate the simulation of hair and facial hair movements for Wukong
